INTRODUCTION

To convert a fraction to a decimal, you can, for example:

• extpand the denominator to 10, 100, 1000, etc.:

$\frac{1}{4}=\frac{25}{100}=0.25$

$\frac{7}{8}=\frac{875}{1000}=0.875$

$\frac{3}{5}=\frac{6}{10}=0.6$

• divide the numerator by the denominator

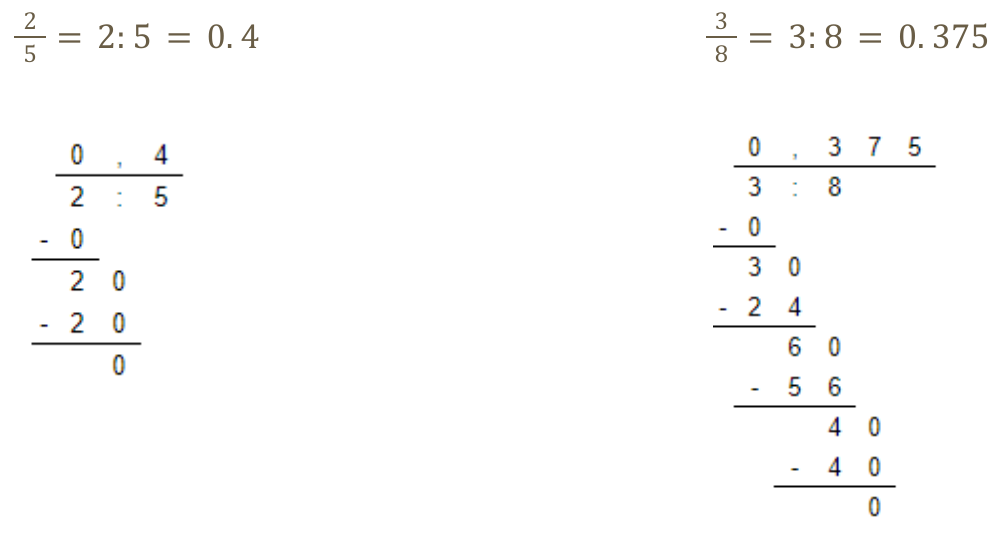
However, there are common fractions whose:

• the denominator cannot be expanded to 10, 100, 1000 …,
• there is no end to dividing the numerator by the denominator

EXAMPLE

Fraction $\frac{2}{11}$ after dividing the numerator by the denominator, it has the form: 0,1818181818…

We say about such fractions that:

• May infinite decimal expansion,
• And period of this expansion is a repeating sequence of digits – in the example above, the period is (18)

PYTHON CODE

def convert_fraction(fraction):
    numerator, denominator = fraction.split("/")
    numerator = int(numerator)
    denominator = int(denominator)

    decimal = numerator / denominator

    remainder = numerator % denominator
    remainders_seen = {}
    repeating_digits = []

    while remainder not in remainders_seen:
        remainders_seen[remainder] = len(repeating_digits)
        repeating_digits.append(str(int(10 * remainder / denominator)))
        remainder = 10 * remainder % denominator

    repeating_length = len(repeating_digits) - remainders_seen[remainder]

    if remainder == 0:
        return str(decimal)
    else:
        repeating_sequence = "".join(repeating_digits[remainders_seen[remainder]:])
        return f"{decimal}  ---> repeating sequence: {''.join(repeating_digits[:remainders_seen[remainder]])}({repeating_sequence})  number of digits in sequence: {repeating_length} "

fraction = str(input("Enter a fraction in the format numerator/denominator, for example 2/3: "))
result = convert_fraction(fraction)
print(result)

⬆️⬆️⬆️ Zobacz w Google Colaboratory

HOW THE CODE WORKS?

1. The program defines a function named „convert_fraction” that takes one argument, a string representing a fraction in the format of „numerator/denominator”.
2. Inside the function, it splits the input string into numerator and denominator variables using the „/” character.
3. The numerator and denominator variables are then converted to integers.
4. The program calculates the decimal value of the fraction by dividing the numerator by the denominator and storing it in a variable named „decimal”.
5. The program calculates the remainder of the fraction by calculating the modulus of the numerator and denominator, and stores it in a variable named „remainder”.
6. The program initializes an empty dictionary called „remainders_seen” and an empty list called „repeating_digits”.
7. The program enters a while loop that continues until the remainder is found in the „remainders_seen” dictionary.
8. Inside the while loop, the program adds the current remainder to the „remainders_seen” dictionary with its index in the „repeating_digits” list as the value.
9. The program appends a string representation of the next digit in the repeating decimal sequence to the „repeating_digits” list.
10. The program calculates a new remainder by multiplying the current remainder by 10 and taking the modulus of the denominator.
11. Once the while loop has completed, the length of the repeating sequence is determined by subtracting the index of the first occurrence of the remainder in the „remainders_seen” dictionary from the length of the „repeating_digits” list.
12. If the remainder is zero, the program returns the decimal value of the fraction as a string.
13. Otherwise, the program creates a string representation of the repeating decimal sequence and returns it along with the decimal value and the number of digits in the repeating sequence as a formatted string.
14. The program prompts the user to enter a fraction in the specified format using the „input” function and stores the result in a variable named „fraction”.
15. The program calls the „convert_fraction” function with the user input as the argument and stores the result in a variable named „result”.
16. The program prints the result to the console using the „print” function